Is Confusion Matrix really Confusing?
Confusion matrix, Precision, Recall, F1-score.
After reading this blog, I am sure you will not be confused with the confusion matrix.
Let's get started.
The confusion matrix is the table that is used to describe the performance of the model.
We can use accuracy as a metric to analyze the performance of the model, then why confusion matrix???
What is the need for Confusion matrix???
So to understand this let us consider an example of the cancer prediction model.
Since this is a binary classification model its job is to detect cancerous patients based on some features. Considering that only a few, get cancer out of millions of population we consider only 1% of the data provided has cancer positive.
Having cancer is labeled as 1 and not cancer labeled as 0,
An interesting thing to note here is if a system gives the prediction as all 0’s, even then the prediction accuracy will be 99%. It is similar to writing print(0) in model output. This will have an accuracy of 99%.
But this is not correct right??
Now that you know what is the problem and the need for a new metric to help in this situation, let us see how the confusion matrix solves this problem.
Let us consider an example with a classification dataset having 1000 data points.
We get the below confusion matrix:
There will be two classes 1 and 0.
1 would mean the person has cancer, and 0 would mean they don't have cancer.
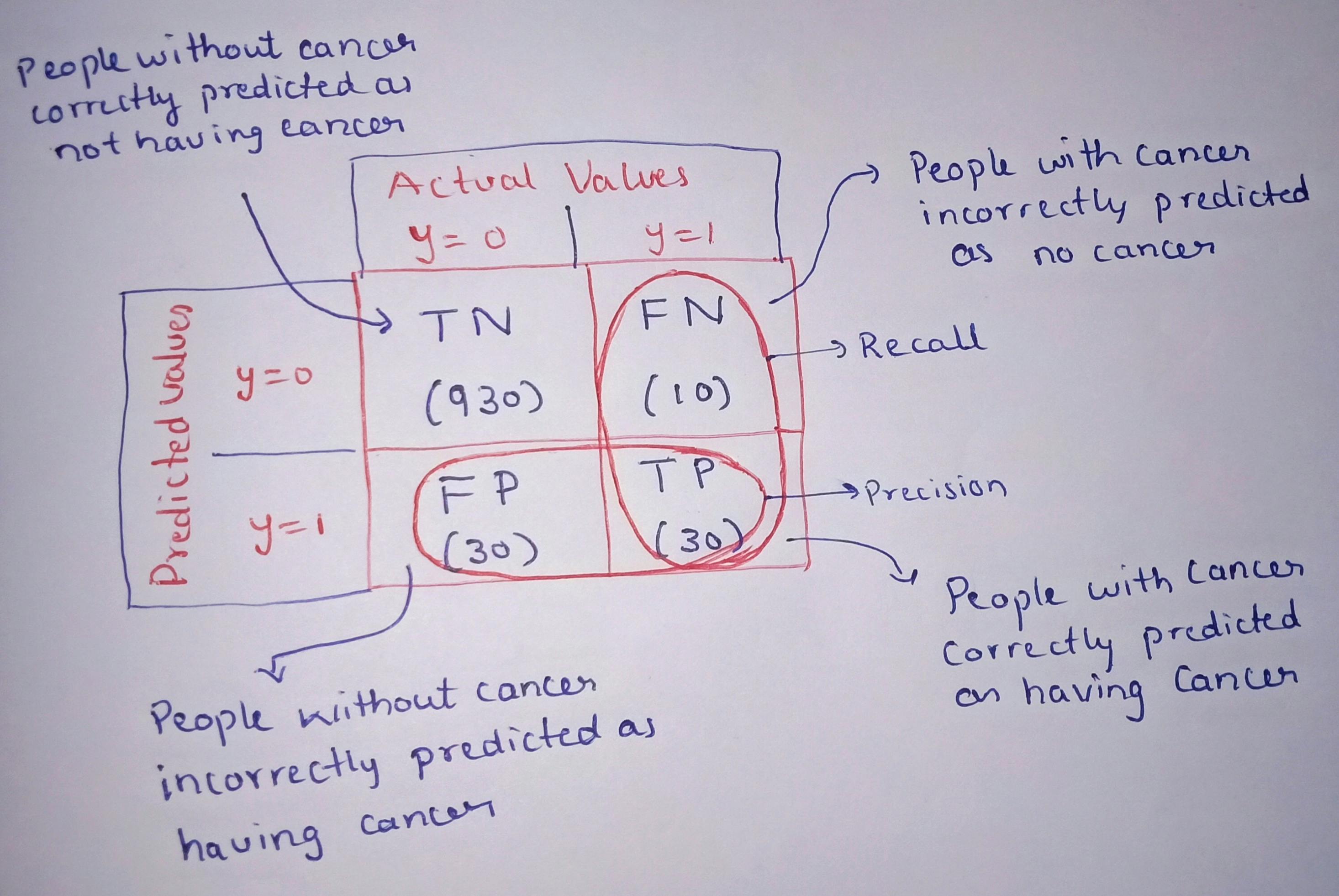
By seeing this table we have 4 different combinations of predicted and actual values. Let us consider predicted values as Positive and Negative and actual values as True and False.
Just hold on,,, this is easy and you will understand....
True Positive:
Interpretation: Model predicted positive and it’s true.
Example understanding: The model predicted that a person has cancer and a person actually has it.
True Negative:
Interpretation: Model predicted negative and it’s true.
Example understanding: The model predicted that a person does not have cancer and he actually doesn't have cancer.
False Positive:
Interpretation: Model predicted positive and it’s false.
Example understanding: The model predicted that a person has cancer but he actually doesn't have cancer.
False Negative:
Interpretation: Model predicted negative and it’s false.
Example understanding: The model predicted that a person does not have cancer and person actually has cancer.
Precision:
Out of all the positive classes we have predicted correctly, how many are actually positive.

Recall:
Out of all the positive classes, how much we predicted correctly.
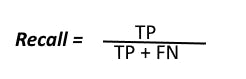
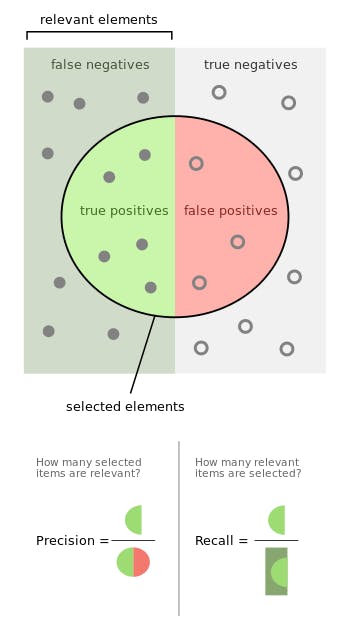 Image credit: Wikipedia
Image credit: Wikipedia
Calculating precision and recall for the above table.
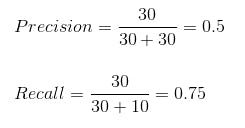
Let's compare this with accuracy.
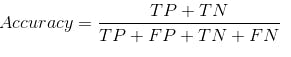
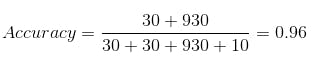
The model got an accuracy of 96% but the precision of 0.5 and recall of 0.75
which means that 50% percent of the correctly predicted cases turned out to be cancer cases. Whereas 75% of the cancer positives were successfully predicted by our model.
Consider an example where prediction is replaced by print(0). so that we get 0 every time.
| Actual y=0 | Actual y=1 | |
| Predicted y = 0 | 914 | 86 |
| Predicted y = 1 | 0 | 0 |
Here accuracy will be 91.4% but what happens to Precision and recall??
Precision becomes 0 since TP is 0.
Recall becomes 0 since TP is 0.
This is a classic example to understand Precision and Recall.
So now you understand why accuracy is not so useful for imbalanced dataset and how Precision and Recall plays a key role.
One important thing is to understand is, when to use Precision and when to use Recall??
Precision is a useful metric where False Positive is of greater importance than False Negatives.
For example, In recommendation systems like Youtube, Google this is an important metric, where the wrong recommendations may cause users to leave the platform.
Recall is a useful metric where False Negative is of greater importance than False Positive. For example, In the medical field, detecting patients without a disease positive can be tolerated to an extent but patients with disease should always be predicted.
So what is the case when we are not sure whether to use Precision or Recall??
or what to do when one of the two is high, whether the model is good???
To answer this let us see what is F1 score.
F1-score is a harmonic mean of Precision and Recall, and it is a high value when Precision is equal to Recall.
Why not normal arithmetic mean instead of harmonic mean??
Because arithmetic mean gives high value when one of the two is high value but harmonic mean will be high only when both are almost equal.
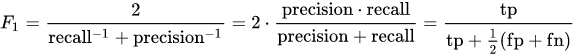
So from our example, the F1 score becomes
F1 = 2TP / (2TP + FP + FN) = 230 / (230 + 30 + 10) = 0.6
I believe after reading this Confusion matrix is not so confusing anymore!
Hope you learned something new here and don't forget to comment below your thoughts. Thanks for reading!
Keep learning, Keep Growing.
